This post explains how to price Hearthstone cards with a unique ability. This method is illustrated through the appraisal of two cards with unique abilities, Edwin VanCleef and Twilight Drake, as they have drastically different abilities. As we will see, our analysis concludes that VanCleef is clearly an undervalued card whereas Twilight Drake has a fair price.
This post is part of a series of posts about applying machine learning to Hearthstone. This series so far has the following posts:
- How to price Hearthstone cards: Presents the card pricing model used in the follow-up posts to find undervalued cards.
- How to find undervalued cards automatically: Builds on the pricing model to find undervalued cards automatically.
- Pricing special cards: Showcases how to appraise the cost of cards that have complex effects, like VanCleef.
- Predicting your Hearthstone?s opponent deck: Demonstrates how to use machine learning to predict what the opponent will play.
- Predicting Hearthstone game outcomes with machine learning: Discusses how to apply machine learning to predict game outcomes (this blog post).
Note The analysis discussed in this post was done in 2014. While Hearthstone has changed a lot since then, the principles remain the same and the analysis can easily be applied to the latest version and to any other card-collecting game.
Last edit This post was last edited in October 2016. The introduction was fully rewritten to reflect the current state of the research.
Edwin VanCleef is a steal

As visible on the text of the card, VanCleef’s ability is pretty straightforward. For every card you played earlier in the turn, VanCleef will get +2/+2. When taken to the extreme, you can get an insanely large creature. For example, you can get a 10/10 creature on turn 3 or even a 216/40 VanCleef with a little help.
So is VanCleef undervalued? To find out, first let’s figure out after which size (4/4, 6/6, …) VanCleef becomes undervalued. To compute the real value for each size, we will multiply the attack power and health points by the base coefficients we figured out using the method explained in the previous post.
The updated model tells us that a health point is worth 0.81 mana and an attack point is worth 1.14 mana. Applying these to every (reasonable) VanCleef size gives us the following table:
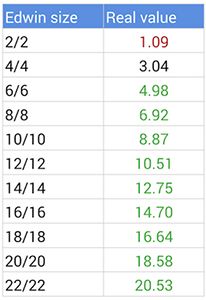
As one can see, VanCleef can become an undervalued card as soon as it hits 4/4 and clearly becomes an undervalued card from 6/6. This is in theory.
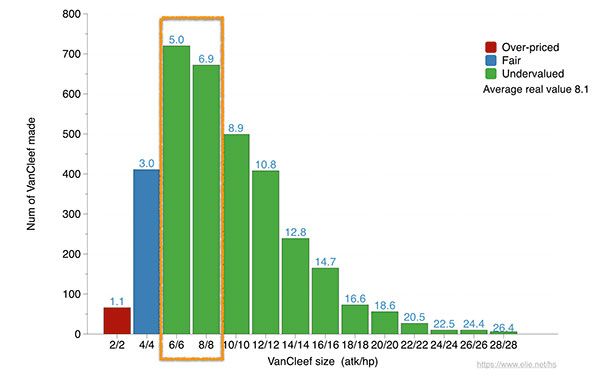
To know if in practice it is an undervalued card, we will have to look at how the card is played. To do so, I processed 100,000 game replays (which I got from a reliable source) and gathered statistics about Edwin’s size every time it was played (~3500 times).
VanCleef’s average size is 9.3/9.3, which put its real value, on average, at roughly 8.1 (s visible in the chart below, which shows a breakdown of the popularity of VanCleef of various sizes. While that might be a little too expensive and make it unplayable, increasing the price of VanCleef to 5 or 6 could make sense. Let me know what you think is the right price for VanCleef:
Twilight drake
At the opposite of the spectrum, the mana cost of Twilight Drake is fair.

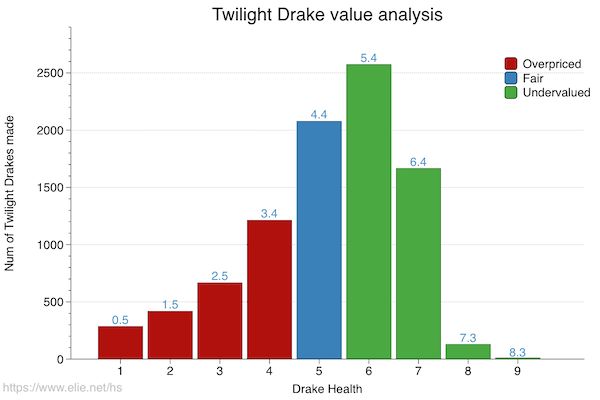
Following the same approach, we can establish that the Drake becomes a good bargain when it reaches 5 to 6 health, as visible in the table below. Parsing the same 100,000 replays allowed me to find 9000 instances where a Drake was played.
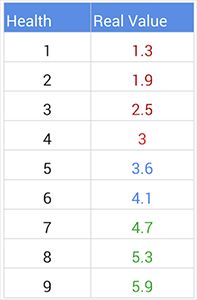
A breakdown of the Drake’s health size by popularity is visible in the figure below. As one can see, the current version of the Drake is right on spot. On average, the real value of the Drake is 3.7, which can be rounded to 4 and that is the value of the card.
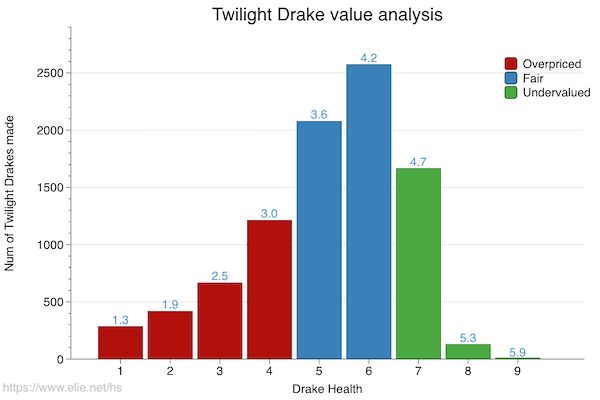
The fact that our analysis found the same optimal value as the one Blizzard used makes me believe that they are using roughly the same approach than us except that they have way better data :)
Twilight drake before the nerf
As a final note, it is interesting to look at the effect the nerf had on the Drake. Before the patch, the Drake was a 1/1 and it gained +1/+1 for each card in the hand. Assuming the distribution of the Drake’s size was the same, the average real price for the Drake was 4.56 as visible in the chart below.
This led us to the conclusion that the nerf was effective as it pushed the average mana cost to 4, which is the Drake face value.
Another nerf option would have been to raise the card price to 5 mana; however, that is a worse option. The pre-nerf distribution curve, displayed below, clearly shows that changing the effect rather than increasing the price was better as it removed some of the card variance: the smaller Drake is less weak now (1.3 vs 0.5) and the most powerful one is not as powerful as before (6.4 vs 7.3 before).
In the next post, we will switch gear and focus on how to predict what the opponent is going to play.
Thanks for reading this post to the end! If you enjoyed it, don’t forget to share it on your favorite social network so your friends and colleagues can too.
To get notified when the next post is online, follow me on Twitter, Facebook, Google+. You can also get the full posts directly in your inbox by subscribing to the mailing list or the RSS feed.




