How to appraise Hearthstone card values

In 2014, I became an avid player of Hearthstone: Heroes of Warcraft, Blizzard Entertainment’s collectible card game. As my understanding of the game deepened, I started to become interested in developing new techniques to find game design flaws.

What makes this endeavor interesting, besides being the first of its kind, is that the game design flaws weren’t uncovered with traditional hacking techniques, such as reverse engineering. Instead, we relied on machine learning and data mining to do so.

After showing an early version of this work to a few friends, it became clear that these results were novel and potentially interesting, not only to Hearthstone aficionados but also to people interested in game design and machine learning. This is why I decided to make this research public and I have written a series of blog posts that summarize my key findings.

This post, the first of the series, discusses the underlying pricing model I developed for Hearthstone. Like any economic model, its goal is to model how goods (in this case, cards) are priced in a given market and to predict how the market and market actors will behave (games and players).

This model is important because it is the foundation that we will build on to reverse engineer effectively each card’s true mana cost, allowing us to detect overpowered cards. Later, we will also use it to help feature engineering of our model to predict game outcomes.

Overall my series of posts about Hearthstone and machine learning is made of the following posts:

1. How to price Hearthstone cards: Presents the card pricing model used in the follow-up posts to find undervalued cards (this post).
2. How to find undervalued cards automatically: Builds on the pricing model to find undervalued cards automatically.
3. Pricing special cards: Showcases how to appraise the cost of cards that have complex effects, like VanCleef.
4. Predicting your Hearthstone’s opponent deck: Demonstrates how to use machine learning to predict what the opponent will play.
5. Predicting Hearthstone game outcomes with machine learning: Discusses how to apply machine learning to predict game outcomes.

Note that if you prefer a talk format, Celine and I presented the card appraisal techniques discussed in this post and the opponent deck prediction attack at Defcon22 (slides and video). Also, if you prefer a more scientific treatment, the opponent deck prediction attack and the game outcome prediction were published in a research paper.

Last edit This post was last edited in October 2016. The introduction was rewritten to reflect the latest research and to correct various aspects of the typography.

Model assumptions and limitations

Before we delve into how the pricing model works, let’s review the assumptions it’s built on. This is very important, because valid assumptions ensure model correctness. Looking at the assumptions also helps in understanding its limitations. Overall the model rests on the following five assumptions about Hearthstone game design:

1. The mana cost of a card is proportional to its power: This assumption models that, for example, a two-mana card is more powerful than a one-mana card. If this were not true, then there would be low-mana cards more powerful than higher-mana cards, which would lead players to play only the cheaper and more efficient low-mana cards. In practice, people play high-mana cards and Blizzard nerfs cards that are too cost-efficient.

2. The power of cards increases roughly linearly: This assumption implies that a two-mana card is roughly twice as powerful as a one-mana card, and a three-mana card is three times more powerful than a one-mana card and so forth. The reasoning behind this assumption is the following: a. If the power of Hearthstone cards increased exponentially, then any late-game card (e.g., a seven-mana card) would be able to overpower a board of early-game cards, such as a board full of one- and two-mana cards. b. Given the success of decks such as the Zoo deck, which plays a lot of cheap cards, this is clearly not the case. Similarly, if the power of cards increased sub-linearly, then any late-game focus decks (control decks) would have no chance of winning. This is clearly not the case either as control decks are also able to win games. As discussed in a follow-up post, the evolution of game metrics over time supports this linear-cost hypothesis.

3. Card effects have a constant price: This implies that an attribute such as spell power has the same cost, regardless of whether it was for a one-mana card, a two-mana card, or a ten-mana card. Some effects, such as spell power, can be stacked: +1 spell power adds the effect of one spell power, +2 spell power adds two spell powers, and so on.

   To account for this variable part, effect costs are computed as a dot product: attribute cost = quantity x attribute coefficient where quantity is the number of times the attribute is applied (e.g., 3 for a +3 spell power effect) and attribute coefficient is the cost of a single instance of the attribute.

   This linear modeling is consistent with assumption #2. Some effects are a factor of the attack or health statistics, including charge and windfury. These are computed using the same dot product except that the quantity is the value of the statistic they depend on. For example, if a card has the charge ability and 2 attack points, then the cost of the charge is computed as 2 x charge.

4. A card has an intrinsic value: Given that the number of cards drawn is constrained by the game, the simple fact of holding a card gives a player an advantage. This advantage is captured by adding an intrinsic value to each card that is constant.

5. The cost of a card is the sum of its attributes: This assumption implies that the mana cost of a card is exclusively based on what the card’s attributes are. Given that Hearthstone is a closed system with no external forces, there’s no reason to account for unknown or hidden variables that would affect the cards or the game.

The model discussed in this post is meant to be the simplest representation of the game possible. By design, it does not model or capture the board or player state (such as the number of creatures in play or the size of the players’ hands), which makes it unsuitable for estimating the pricing of cards that depend on these (e.g. Twilight Drake).

Not taking into account the board state is a deliberate decision that was motivated by the fact that a model without it still works well for most cards. It is easy to understand and does not rely on information that is difficult to get. However, it will be easy to extend this model to do so as discussed in this blog post.

Hearthstone pricing model

The best way to model our assumptions is to use a linear model, where the mana cost of a card is equal to the sum of its attributes (core stats, abilities, and effects) plus the intrinsic value of the card (intercept). The overall formula is

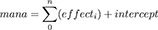
Pricing the Chillwind Yeti

Let’s illustrate how to apply this model to a basic card - a card with no special effects - called the “Chillwind Yeti”:

As visible in the illustration above, because the Yeti is a basic card, it has only the two basic attributes: attack and health. Therefore, its mana cost (6) only depends on its health, attack, and intrinsic value. That means that we can model the price of the Yeti like this:

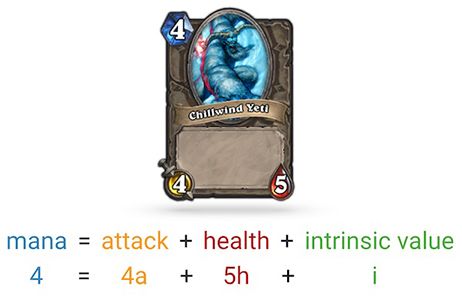
Here a is a coefficient that represents the mana cost that Blizzard associated with 1 attack point. Similarly, h is the mana cost of a health point and i the cost associated with having a card.

Note that coefficients are mostly between 0 and 1. For example, the price of a health point is 0.4 mana. We will see in the next post how to find these values. For now, let’s just view them as constant values.

Comparing cards

This decomposition allows us to compare the value of two cards very easily. To demonstrate this, let’s compare the Boulderfist Ogre (another basic card) with the Yeti.

First, we decompose the 6 mana cost of the “Boulderfist Ogre” as 6a + 7h + i as you can see in the diagram above.

Then, to make things easy to compare, we normalize the equations by dividing by the number of mana they cost (6 and 4, respectively) so we can see clearly how much health and attack power we get for 1 mana.

Doing so, allows us to realize that we get better value out of a Chillwind Yeti than a Boulderfist Ogre: 0.09 health per mana point invested.

Pyroblast vs Fireball

As a second example, let’s compare a Fireball with a Pyroblast:

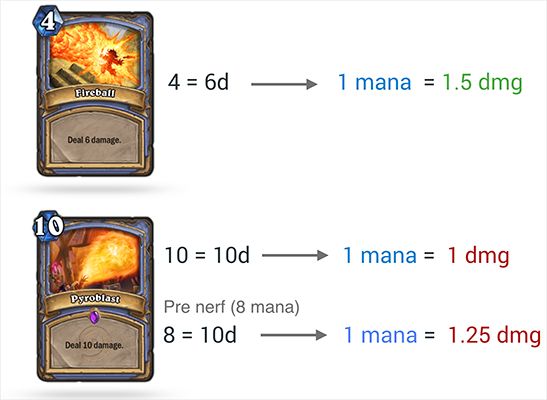
As you can see in the figure above, despite having a lower mana cost (6 vs 10), the Fireball card is actually better value than the Pyroblast: you get 0.5 more damage per mana cost invested.

The nerf/change that Blizzard implemented in 2014 actually made the situation even more inconsistent as illustrated above. If the “right” price is 1 damage per mana cost, then a Fireball should be 4 damage or cost 6 mana, or a Pyroblast should be 15 damage for 10 mana if the Fireball ratio is the right one.

I hope these examples demonstrate why this model is reasonable and how it can be used to compare quickly the real value of a card, as opposed to its face value.

In the next post, I’ll explain how we can determine the value of the attribute coefficients using the least squares method, how to compare cards that have different attributes, and how to combine all of this to find the most overpowered cards.

Thanks for reading this post to the end! If you enjoyed it, don’t forget to share it on your favorite social network so your friends and colleagues can too.

To get notified when the next post is online, follow me on Twitter, Facebook, Google+. You can also get the full posts directly in your inbox by subscribing to the mailing list or the RSS feed.